| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- driver
- NP
- GPT
- ubuntu
- 설치
- Dism
- ISO
- Download
- UEFI
- win to go
- 파티션 복구
- 전체출력
- cell 너비
- 행열크기
- jupyternotebook
- 윈투고
- WF
- 드라이버
- ImageX
- numpy
- 가로 크기
- LPD
- EPSON
- win to usb
- mbr
- 5690
- Today
- Total
conductor
중심 극한 정리 본문
중심극한정리
central limit theorem
CLT
# 표본의 평균, 모집단의 평균과 같다.
# (큰 수의 법칙)확률시행 큰 수로 반복 시 값은 평균값으로 수렴
# 30이상 표본의 평균들 반복, 분포보면 정규분포(예외가능)
동일한 확률분포를 가진
독립 확률변수 n개의
평균의 분포 n이 적당히 크다면 ((평균의 분포가?))
정규분포에 가까워진다는 정리
( in 확률론 & 통계학 )
수학자 피에르 시몽 라플라스 1774~1786 정리 발견 및 증명 시도.
표본 n 20 30
------------------
린데베르그-레비 중심극한정리 ( 같은 분포를 가지는 독립 확률 변수 )
만약 확률 변수 X1, X2, ... 들이
1. 서로 독립적이고,
2. 같은 확률 분포를 가지고,
3. 그 확률 분포의 기댓값 μ와 표준편차 σ가 유한하다면,
평균 Sn = ( X1 + ... + Xn ) / n의 분포는 기댓값 μ, 표준편차 σ/√n인 정규분포 N( μ , σ²/n )에
분포수렴한다.

랴푸노프 중심극한정리 (기본정리, 같은분포를 가지는 조건 완화)
만약 각 확률변수 Xi가
1. 서로 독립적이고,
2. 각각 유한한 평균과 분산 μi , σi²을 가지며,
3. ( 라푸노프 조건 ) 이 성립할 때,
si² = ∑ ((j ≤ i)) σj² 를 정의하면 어떤 양의 실수 δ에 대하여
lim ((n → ∞)) 1 / s n ^ (2 + δ) ∑ n ((i = 1)) E [ | X i − μ i | ^( 2 + δ )] = 0
가 성립할 때,
∑ i ( X i − μ i ) / s i 의 분포는 n이 커질수록 표준정규분포에 분포수렴한다.

린데베르그 중심극한정리 ( 라푸노프 중심극한정리 조금 더 완화 )
만약 각 확률변수 Xi가
1. 서로 독립적이고,
2. 각각 유한한 평균과 분산 μi , σi²을 가지며,
3. (린데베르그 조건) 다음 공식이 성립할 때,

라푸노프 중심극한정리와 같은 결론을 내릴 수 있다. 여기서 1{...}는 지시함수이다.
마팅게일 중심극한정리 (Xi들이 독립변수가 아니므로 위 정리들은 성립하지 않음. 그러나. )
이 경우에도 다음과 같은 마팅게일 중심극한 정리가 성립한다.
만약 각 확률변수 Xi가
1. 마팅게일을 이루며,
2. n → ∞ 인 극한에서 다음이 성립하고,
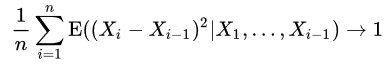
3. 모든 ϵ > 0 에 대하여 n → ∞ 인 극한에서 다음이 성립할 경우,
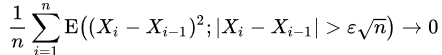
은 n → ∞ 인 극한에서 표준정규분포로 분포수렴한다.

여기서 E(A|B)는 조건부 기댓값, E(A;B)는 제한 기댓값이다.
----------------
5. 중심극한정리란
분산이 유한한 모집단에서 샘플링된 표본 데이터는 표본 데이터의 크기가 커질수록 정규분포의 형태를 띄어간다는 것. 즉, n이 무한한 값으로 커져갈수록 정규분포에 가까워진다는 것이다.
중심극한정리의 맹점 : 중심극한정리를 맹신하여 모든 상황이 정규분포에 수렴한다는 가정을 하는 것. 모집단의 데이터가 충분하지 않거나 특수한 도메인의 경우에는 정규분포에 수렴하지 않을 수 있다.
큰 수의 법칙이란 : 어떤 확률을 가진 시행을 큰 수로 반복했을 때, 그 사건의 결과는 평균의 값으로 수렴하게 된다는 것. 예를 들어 앞면 뒷면을 가진 동전을 여러번 던졌을때, 그 비율은 1:1로 수렴하게 되는것이다.
Universal Approximation Theorem : Deep Learning에서의 중심극한정리라고 말할 수 있는 개념이다. 존재할 수 있는 모든 함수 f(x)는 인공신경망으로 반드시 수렴시킬 수 있다는 간단한 이론이다. 딥 러닝을 연구하는 여러 유명인사들이 자주 강조하는 개념이다. DL을 처음 시작할 때 직접 코딩해보는것도 도움이 된다.
